Enero

Clase N:15

Cálculo de máximos y mínimos absolutos de una función

Si z=f(x,y) es una función continua en una región D cerrada y acotada,

ya hemos dicho que f alcanza sus valores máximo y mínimo absolutos. Según lo que acabamos de ver, estos valores se alcanzarán en:

Puntos frontera de D
Puntos críticos de f (puntos interiores de D en los que fx=fy=0, o alguna de ellas no exista).

Calculando f en todos ellos y eligiendo los valores mayor y menor tendremos los valores máximo y mínimo absoluto respectivamente.

Para aplicar el criterio de la segunda derivada:

Hallar las derivadas parciales de f con respecto a x y a y.
Igualar a cero las derivadas parciales encontradas anteriormente y encontrar los puntos críticos.
Hallar las derivadas parciales de segundo orden Fxx; Fxy; Fyy.
Determinar cada segunda derivada en los puntos críticos.

CLASE N.- 16

Multiplicadores de Lagrange

Consideremos un caso bidimensional. Supongamos que tenemos la función, f (x, y), y queremos maximizarla, estando sujeta a la condición:{\ g(x,y)=c,}

g(x,y)= c

donde c es una constante. Podemos visualizar las curvas de nivel de f dadas por{f(x,y)=d_{n}}

f(x,y)= d

para varios valores de dn, y el contorno de g dado por g(x, y) = c. Supongamos que hablamos de la curva de nivel donde g = c.


Entonces, en general, las curvas de nivel de f y g serán distintas, y la curva g = c por lo general interceptará y cruzará muchos contornos de f. En general, moviéndose a través de la línea g=c podemos incrementar o disminuir el valor de f. Sólo cuando g=c (el contorno que estamos siguiendo) toca tangencialmente (no corta) una curva de nivel de f, no se incrementa o disminuye el valor de f.

Esto ocurre en el extremo local restringido y en los puntos de inflexión restringidos de f.


1.- Caso de una única restricción

Observamos que cuando se satisface la restricción y se cumple que:

 

Observemos que la condición equivale a pedir que se satisfaga la restricción.

Condición necesaria (Caso m = 1)

Entonces, si denotamos como Hx L(x ; λ) la hessiana de la función de Lagrange en  respecto de las variables iniciales (no respecto λ) tenemos:

2.- Caso de más de una restricción:

La función L se llama función de Lagrange y los λ, multiplicadores de Lagrange.

Observamos que se añade un multiplicador λ por cada restricción y que cuando se satisfacen todas se cumple que L(λf......λi)=f(x,y)

Observemos que la condición equivale a pedir que se satisfaga la restricción.

Para un mejor entendimiento les dejo este video a mi me ayudo full

Método de los Multiplicadores de Lagrange

Sea g una función de dos variables continuamente diferenciable en un subconjunto del dominio de f. Si (xo , yo ) hace máxima (ó mínima) a f(x,y), sujeta a la condición extra g(x,y) = 0, entonces:

Son colineales, es decir, de igual dirección. En consecuencia existe un escalar λ tal que:

Demostración geométrica: La ecuación g(x,y) = 0 define una curva C que vamos a suponer que posee en cada punto un vector tangente no nulo.

CLASE N: 17

Integrales Múltiples

Una integral múltiple es un tipo de integral definida aplicada a funciones de más de una variable real, por ejemplo, f(x,y) ó f(x,y,z).

Las integrales múltiples están estrechamente relacionadas con las integrales iteradas, las cuales son necesarias para resolver las integrales múltiples. La diferencia entre integrales múltiples e iteradas consiste en que una se refiere al concepto matemático de integral (aplicado a varias variables)

Región de donde parte la integral

INTEGRAL DOBLE:

INTEGRAL TRIPLE:

TIPOS DE REGIONES DE INTEGRACIÓN

REGIONES RECTANGULARES:

Estas integrales pueden denominarse integrales iteradas, debido a que se puede integrar en cualquier orden, manteniendo el mismo resultado.

REGIONES MÁS GENERALES:

  

                                          (a)                                                  (b)

Para el caso a) donde (x) es constante y (y) depende de (x): 

Para el caso b) donde (y) es constante y (x) depende de (y):

TRANSFORMACIONES DE INTEGRALES MÚLTIPLES

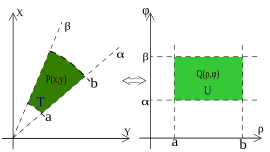
Las transformaciones se las puede a ser a las siguientes coordenada:

1. Coordenadas Rectangulares a Coordenadas Polares

2. Coordenadas Rectangulares a Coordenadas Cilíndricas

resuemiendo los jacovianos de las transformaciones de coordenadas rectangulares a cuaquier sistema quedan asi  

Se utilizan cuando en las ecuacion ordinaria existen variables independientes elevadas a una potencia mayor a 1

CLASE N: 18

Ejercicios de repaso 

• 
  
• 4. Hallar , para un volumen representado por una esfera con centro en el origen y radio a.

Se pudiera resolver directamente por coordenadas cartesianas, pero se puede observar que el volumen de integración es una esfera por lo que pudiéramos intentar resolver por coordenadas esféricas.

La ecuación general de una esfera con centro en el origen y radio r es:

El diferencial de volumen en coordenadas esféricas es:

Por lo que la integral queda de la siguiente forma:

donde:

2.-do ejercicio

calcular el area encerrada por las ecuaciones r=4sin(Theta) y r=4cos(theta)

---

3er EJERCICIO

Ejemplo 4 

 

   

Aqui les dejo un link donde pueden encontrar otrs ejercicios que ya están resueltos de manera fácil y complicada para comprender que existen varias formas de resolverlos 

EJERCICIOS RESUELTOS

CLASE N: 19

Resolución de ejercicios en coordenadas rectangulares a polares de superficies y volúmenes

Ejercicio 1



Ejercicio 2

Transformación de coordenadas rectangulares a cilíndricas y a esféricas 

Coordenadas Cilíndricas

En el sistemas de coordenadas cilíndricas un punto P del espacio tridimensional está representado por la terna ordenada (r,θ,z), donde r y el θ son las coordenadas polares de la proyección de P en el plano xy y z es la distancia dirigida del plano xy a P.

CLASE N: 20

APLICACIONES DE LAS INTEGRALES MULTIPLES

1. Cálculo de áreas planas.
2. Cálculo de volúmenes.
3. Cálculo del centro de masa.
4.Cálculo de momento de inercia.
5. Cálculo de probabilidad con distribución normal


Centro de masa:

Caso 1:


CASO DISCRETO







Si tiene "n" partículas





Caso 2:


CASO CONTINUO







Importante

estos datos generalmente te dan antes de comenzar a resolver el problema y es necesario identificarlos bien 

Distribución de masa lineal:

este caso nos da el incremento maximo de la lmasa con respecto a longitud




Distribución de masa superficial:

este caso nos da el máximo incremento de la masa en relación al área de una región

Distribución de masa volumétrica:

este caso nos da el máximo incremento de la masa en relación al volumen



Momento de Inercia

CLASE N: 21

CLASE N: 22

Campos Vectoriales

Sirven para representar fenómenos naturales tales como:
-Rapidez y dirección del viento
-Magnitud del campo gravitacional en diferentes lugares sobre la superficie terrestre




Un campo vectorial se define como una función que se define sobre un vector en Rn, es decir, un vector que se transforma en otro vector gracias a una función f:




Considerando un plano:


Sea D un conjunto en R2, una región plana. Un campo vectorial sobre R2 es una función F que asigna a cada punto (x,y) en D un vector bidimensional F(x,y).








Considerando un espacio:


Sea E un subconjunto de R3. Un campo vectorial sobre R3 es una función F que asigna a cada punto (x,y,z) en D un vector bidimensional F(x,y,z).

CAMPOS CONCERVATIVOS

Los campos de gradientes son conservativos por definición, y la función de la cual derivan es una función potencial (notar que ésta queda definida a menos de una constante, o sea que en realidad se tiene una familia de funciones potenciales).

para identificar de forma sensilla si un campo es o no concervartivo recurrimos al calculo del rotacional de la funcion el cual debe dar cero

ROT(F)= 0

ROTACIONAL Y DIVEGENTE DE UN CAMPO ESCALAR

Estos procesos se difenrencian entre si pues el rotacional nos da como resultado un vector y el divergente nos da como resultado un product