Comenzamos
Clase #1
Indicaciones generales de la materia y equivalentes
Lo principal que se debe tener en cuenta en clasesValores tales como: respeto, honestidad, responsabilidad, compañerismo.
Actividades y tareas: donde se especifica la creación del portafolio estudiantil y se establece los parámetros de calificación.
Parámetros de calificaciones en el semestre actual
Actividades, tareas y portafolio --- > 20%
Evaluación 1------------ >20%
Evaluación 2------------> 20%
Examen --------------> 40%
Clase #2
Funciones Implícitas1.- En R² una función es implícita cuando F(x,y) = 0 y existen dos posibilidades:
y = f(x)
x = g(y)
Ejemplo:
x² + y² - 9= 0
x² + y² - 9= 0
x=sqrt(9-y²)
En ambos casos deberemos analizar las raices para obtener un valor positivo y negativo por parte de la raiz
Generalmente las funciones implícitas de dos variables representan una curva en el plano (R²)
Generalmente las funciones implícitas de dos variables representan una curva en el plano (R²)
2.- En R³ una función es implícita cuando F(x, y, z)=0
En este caso analizaremos el plano que se generara dependiendo de la generatiz en un plano cartesiano en el espacio
En los gráficos se analizo la función cuando una variable independiente se iguala a cero lo cual se va a considerar como la generatriz en el espacio.
Sistemas de funciones implícitas
F(x,y) = 0
G(x.y) = 0
Cada función representa una curva, entonces la intersección de estas curvas generan 1 o más puntos de intersección.
En R3
F(x.y.z) = 0 Función implícita de 3 variables.
Estas funciones representan superficies, cabe mencionar que la generatriz es paralela al eje que no aparece en la función.

Si se tienen sistemas de 3 funciones implícitas, la solución son puntos en R3.
Ax + By + Cz + D = 0 Es una función implícita de primer grado y representa un plano cuya generatriz no es paralela a ningún eje.

Se debe conocer que la intersección de 3 superficies genera puntos.
Clase #3
EL PLANO
Para determinar un plano se necesitan:
Un punto Po(xo,yo,zo) y un vector Ñ(A, B, C) normal al plano.
La ecuación del plano viene entonces dada por la relación:
A(x - xo) + B (y - yo) + C (z - zo) = 0 A.x + B.y + C.z + D = 0 (1)
Donde D = -A.x - B.y - C.z
Se pueden considerar varios casos particulares según que uno o dos de los coeficientes de la ecuación (1) sean nulos.
a) Plano paralelo al eje OX. Se tiene A = 0 y la ecuación toma la forma:

b) Plano paralelo al eje OY. Se tiene B = 0 y la ecuación general toma la forma:

c) Plano paralelo al eje OZ. Se tiene C = 0 y la ecuación general toma la forma:

d) Plano que pasa por el origen. Se tiene D = 0 y la ecuación general toma la forma:
A.x + B.y + C.z = 0
e) Plano perpendicular al eje OZ. Se tiene en este caso A = 0, B = 0 y la ecuación general toma la forma:

f) Plano perpendicular al eje OY o, lo que es igual, paralelo al plano XOZ. Se tiene en este caso A = 0, C = 0 y la ecuación general toma la forma:
B.y + D = 0 ; y = Cte
g) Plano perpendicular al eje OX o, lo que es igual, paralelo al plano YOZ. Se tiene en este caso B = 0, C = 0 y la ecuación general toma la forma:
A.x + D = 0 ; x = Cte.
ECUACIÓN VECTORIAL
Ésta expresa una recta en términos de 2 vectores: el vector posición de un punto cualquiera de la recta (x,y,z), y el vector dirección de la recta(a,b,c) multiplicado por una constante (en este caso lambda).
Este último se obtiene fácilmente, con la diferencia de las coordenadas de dos puntos de la misma.

ECUACIÓN SEGMENTARÍA DE PLANO
Se trata de saber la ecuación del plano que corta a los ejes de coordenadas en los puntos
x = a ; y = b ; z = c.
Según lo anterior se tiene:
Po = (a,0,0)
P1 = (0,b,0)
P2 = (0,0,c)
P = (x,y,z)
Y la ecuación segmentaría del plano quedará en la forma:
y desarrollando el determinante:
ECUACIÓN NORMAL DEL PLANO
Se mediante los cosenos directores.

FACTOR NORMALIZANTE
DISTANCIA DE UN PUNTO AL PLANO
Conociendo los datos de la ecuación normal de un plano y el vector director del punto que se encuentra en el espacio, obtenemos la ecuación que permite obtener la distancia perpendicular de dicho punto al plano.

Un aporte para un mejor entendimiento de los planos
Observaciones:
Si el producto mixto es igual a cero entonces los tres vectores involucrados son COPLANARES.
El producto misto geométricamente representa el volumen del paralelepípedo cuyas aristas son los tres vectores.

La Recta en R³
“Sea L una recta en el espacio, tal que contenga un punto dado Po y sea paralela a las representaciones de un vector dado R.
La recta L es el conjunto de puntos P tal que el vector es paralelo al vector R”
Para una mejor comprensión de este tema aquí les dejo un pequeño vídeo para clarar sus dudas.
Observaciones:
La recta es un caso particular de una CURVA ALABEADA.
Se puede proyectar una recta sobre cualquier plano coordenado.
Ecuación de la recta dados dos puntos

DISTANCIA ENTRE DOS RECTAS

ECUACIÓN DE LA RECTA DADOS 2 PUNTOS
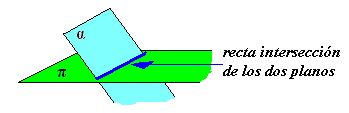
A partir de las ecuaciones generales de los dos planos que se van a intersecar, hallamos la ecuación de la recta que se forma en dicha intersección.

La esfera
Ecuaciones de la esfera
Ecuación cartesiana
En un sistema de coordenadas cartesianas en un espacio euclidiano tridimensional, la ecuación de la esfera unitaria(de radio 1), con centro en el origen, es:Si :{\x^{2}+y^{2}+z^{2}=1\,}

Esta ecuación se obtiene considerando que en el punto M (x, y, z) de la esfera, el vector normal OM es igual a 1.
Generalizando, la esfera de radio r, de centro Ω (a, b, c) tiene como ecuación:
Si :{(x-a)^{2}+(y-b)^{2}+(z-c)^{2}=r^{2}\,}

La ecuación del plano tangente en el punto M (x', y', z') se obtiene mediante el desdoblamiento de las variables: en el caso de la esfera unitaria:
Si: {\ x\cdot x'+y\cdot y'+z\cdot z'=0\,}

y en el segundo ejemplo:
Si: {\ (x-a)\cdot x'+(y-b)\cdot y'+(z-c)\cdot z'=0\,}

Ecuación paramétrica
En un espacio euclidiano tridimensional, los puntos de la superficie esférica pueden ser parametrizados de la siguiente manera:


donde r es el radio, (x0, y0, z0) son las coordenadas del centro y (θ, φ) son los parámetros angulares de la ecuación.





